| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 텐서 플로우 자격증 난이도
- 요양 보호사 시험 어렵 나요
- 패스트캠퍼스AI부트캠프
- 요양 보호사 자격증 취득 방법
- 패스트캠퍼스
- 요양 보호사 자격증
- google tensorflow 자격증
- 요양 보호사 신청
- 구글 텐서 플로우 자격증
- 요양 보호
- 텐서 플로우 자격증 공부
- UpstageAILab
- 요양 보호사 자격증 시험 날짜
- 패스트캠퍼스업스테이지부트캠프
- 요양 보호사
- AI부트캠프
- 텐서 플로우 자격증 준비
- 국시원 요양 보호사
- 보호사
- 요양 보호사 자격증 개요
- 업스테이지패스트캠퍼스
- sqlp 강의
- 국비지원
- Tensorflow 자격증
- 패스트캠퍼스업스테이지에이아이랩
- 텐서 플로우 자격증 합격
- 텐서 플로우 자격증 수기
- 텐서 플로우 자격증
- 텐서 플로 자격증
- upstageailab#국비지원
- Today
- Total
공부법에 관한 모든 것
[ai lab] 딥러닝 본문
딥러닝 모델 학습법에 대해서 알아보자.
인공지능의 작동 원리.

입력값(x,y)을 특정 모델에 넣으면 예측값이 나온다. 이때 model에는 입력값에 가중치를 곱해주는 파라미터가 존재한다. 이후 예측값과 정답 값과의 오차를 loss function을 통해 구한다. loss 값을 기반으로 모델의 파라미터를 loss를 줄여주는 방향으로 업데이트한다.
인공뉴런
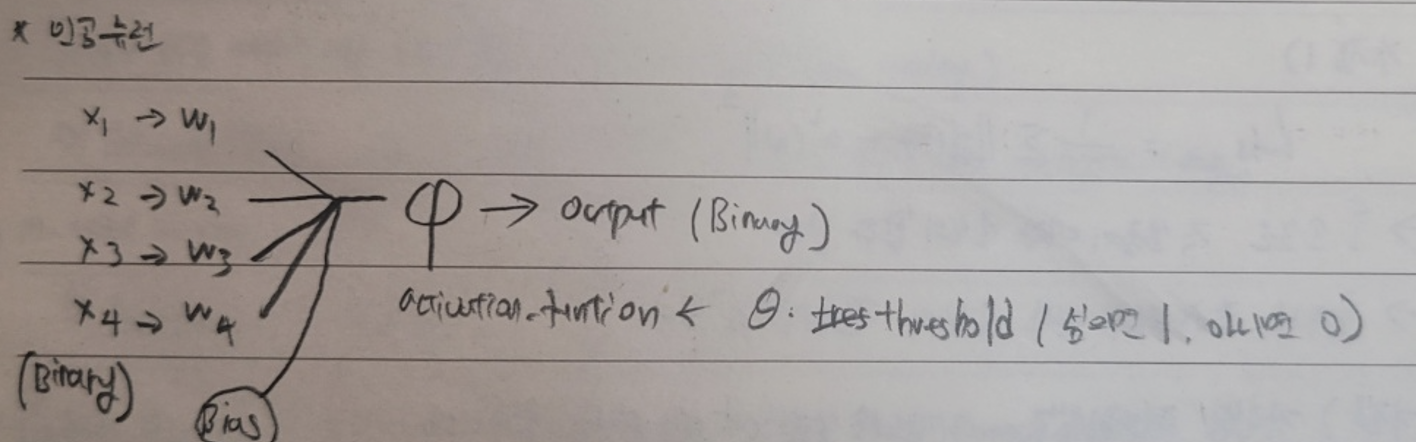
딥러닝은 인공 뉴런을 통해 학습을 한다. 그림은 입력 데이터를 model에 넣어주는 과정을 세분화한 그림이다. 입력된 값들에 가중치(파라미터의 일종)를 곱하고 bias(파라미터)를 더한 값을 activation_ function에 넣어준다. activation_function은 종류가 다양한데 여기선 WX + b의 값이 Theta보다 크면 1을 출력하고 작다면 0을 출력하는 함수이다.
ex) 실례를 통해 작동과정을 살펴보자.

x,y라는 입력 값에 각각 1이 곱해져서 들어온다. theta 값은 1이고 bias는 0이다. 그러면 output이 1인 경우와 0인 경우가 오른쪽 선을 기준으로 나뉘어진다. 즉 인공뉴런을 사용하면 선형 분리를 하는 것이 가능해진다.
MLP

Layer n에 있는 임의의 한 뉴런이 Layer n-1에 있는 모든 뉴런과 연결되어있는 구조를 MLP(Muti-Layer- Perceptron) 이라고 한다.
Activation Function
위에 인공뉴런을 설명할 때 입력 데이터에 가중치를 곱하고 bias를 더한 값을 바로 사용하는 것이 아니라 activation_function에 넣어준 것을 기억할 것이다. 그 이유는 해당 값 자체를 사용하면 선형한 상황을 피할 수 없기 떄문이다. 그러니깐 WX+b 그 자체를 output으로 보내면 그 다음 Layer에 입력값으로 WX+b가 입력값이 될 것이다. 그 Layer의 output은 다시 W(WX+b)+b 꼴이 될 것이다. 즉 선형한 상황 외로는 표현을 할 수가 없다. 따라서 activation func이 필요하고 sigmoid, ReLu, tanh 등 다양한 함수를 사용한다.
경사하강법

경사하강법은 최적화 알고리즘의 일종으로 사용된다. 처음 임의의 파라미터로 예측값을 구하고 결과값과 비교하여 loss를 구했을 때 어떻게 하면 loss를 줄이는 방향으로 파라미터를 업데이트할 수 있을까. 해당 점에서의 기울기들을 구한 다음에 반대 방향으로 파라미터를 업데이트 한다. 맨 밑의 식을 보면 되는데 기존 파라미터에 학습 속도를 의미하는 ir 변수 x 기울기 값을 빼주고 있다.
확률적 경사하강법
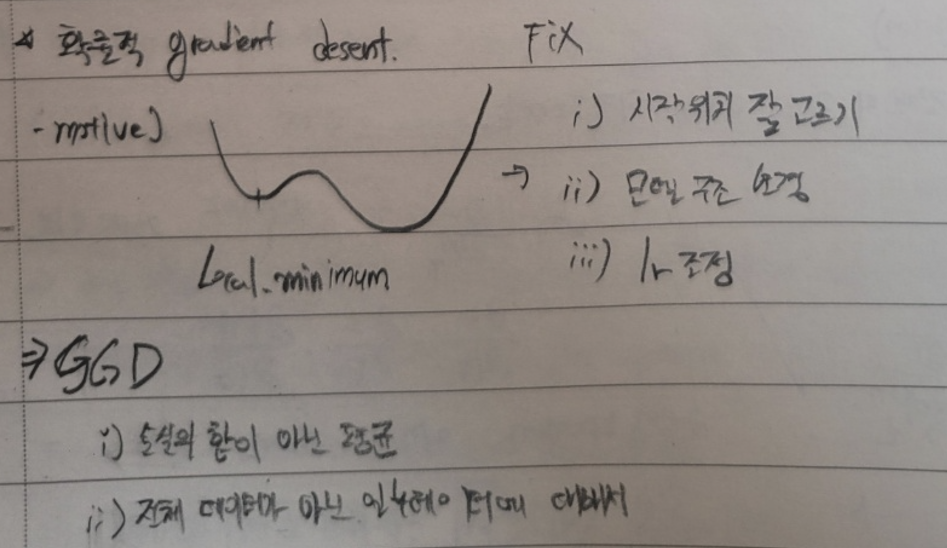
경사하강법의 문제점은 다음과 같다. 손실 함수에 극소값이 존재하면 더이상 업데이트가 되지 않는다. (기울기가 0이여서) 이러한 문제를 해결하기 위해 확률적 경사하강법이라는 기법이 탄생했다. 전체 데이터가 아닌 일부 데이터들을 돌아가며 사용하여 손실 함수를 만들어서 모델 구조를 변경해 극솟값을 없애는 것이다. 해당 방법에 또다른 이점은 전체 데이터를 사용하지 않아 계산량도 적어진다.
cf) 전체 M개의 데이터 중 m개를 골라 학습을 진행하는데 이떄 m을 batch라고 한다.
cf_2) M을 모두 학습한 횟수를 epoch이라고 한다.
sigmoid
활성화 함수로 sigmoid함수를 자주 사용하는데 이유는 다음과 같다. 경사하강법 수식을 보면 미분을 해주어야함을 확인할 수 있고 sigmoid 함수는 모든 지점에서 미분가능한 함수이기 때문이다.
역전파(back propagation)
∇f 라는게 모든 입력 값들에 대한 기울기를 원소로 가지는 matrix이다. 죽 ∇f를 구하기 위해서는 모든 파라미터들에 대한 미분이 필요하다. w,b를 구하는 과정은 SGD(확.경.하)로 가능하지만 모든 파라미터들에 대한 미분을 하는 것은 꽤 많은 연산량을 요구하는 일이다. 이 계산 과정을 간소화해주기 위해 등장한 방식이 역전파이다.
계산 그래프.

전체 편미분을 하기 위해서 작은 단위로 쪼개는 과정을 걷치는데 이때 계산 그래프를 사용한다.
Chain Rule

합성함수 미분을 하는데 쓰이는 테크닉이다. 속함수에 대한 미분을 진행하고 속함수 자체를 미분하는 식으로 합성 함수를 미분할 수 있다. 이때 chain 처럼 소거가 되는 방식이기에 chain rule이라고 한다.
Chain Rule를 적용하여 ∇f 구하기.

앞에서 구한 값을 기억해서 뒤에 위치한 Layer를 업데이트할 때 필요한 연산의 수를 줄여준다.
대표적인 역전파
- '+' 연산의 경우 역전파는 다음과 같이 전개된다.

즉 원래의 신호가 그냥 유지가 되며 전달된다.
- 'x' 연산의 경우 역전파는 다음과 같이 전개된다.

즉 다른 쪽의 edge 값이 곱해진 값이 전달된다.
EX)

이런 형태의 데이터가 존재한다고 가정하자. 그러면 f로 나오는 예측값은 -12이다. 실제 값은 -10이기 때문에 MSE를 사용하면 loss 값은 4가 된다.
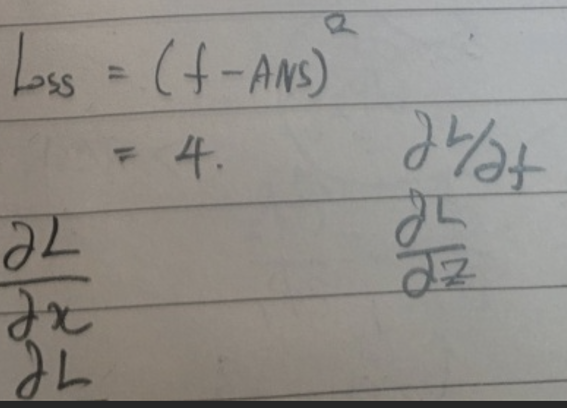
각 파리미터를 업데이트하기 위해서는 각각을 Loss 함수에 대한 편미분을 진행해야 한다.

위에서 언급한 방식으로 각 파라미터의 기울기 값들을 모두 구했다. ir 값을 0.01로 두었을 때 parms - ir x 기울기 연산을 진행하면 업데이트된 파라미터들의 값은 다음과 같다.
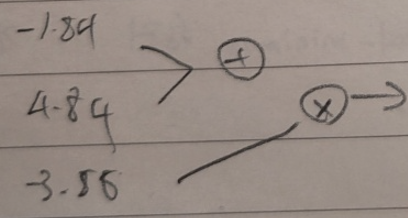
이후 다시 예측값을 구하면 -11.64라는 값이 나오는데 이는 이전의 예측값보다 더 정확한 예측값임을 확인할 수 있다.
역전파의 수학적 증명


이런 느낌으로 전달이 된다. +일 때는 output이 그대로 유지되고 x일 때는 인접한 가중치를 곱하고 넘어감을 확인할 수 있다. 좀더 직관을 발휘하면 활성화 함수의 미분값과 활성화 함수 값 그 자체가 가중치 변화에 따른 비용 함수 변화에 영향을 주는 것을 확인할 수 있다.
즉 미분값이 0에 가까울 경우, 가령 sigmoid 함수에서 y값이 1또는 0에 가까운 경우 가중치의 변화가 손실 함수에 주는 영향이 낮음을 알 수 있다.
손실 함수
마지막으로 어떤 손실 함수를 사용하는 것이 유리한지에 대한 이야기를 하고 글을 마치겠다.
-역전파 관점

아래의 그래프는 sigmoid 함수의 도함수이다. 양 끝쪽으로 갈수록 값이 낮아짐을 확인할 수 있다. 즉 초기 파라미터의 값이 무엇이냐에 따라 학습 속도에 영향을 준다.

cross entropy의 경우 Error가 a_f의 영향을 받지 않기 떄문에 역전파의 관점에서는 cross entropy를 사용하는 것이 학습에 유용하다.
cf) 아니면 모든 지점에서 미분 값이 똑같은 함수를 쓰던가.(LeLU)
-Maxximum Likelihood의 관점
데이터가 확률 함수의 꼴을 가지는 경우 가장 높은 확률을 나오는 지점을 예측값으로 해서 확률 함수 자체를 이동시키는 방식.
-> 결론만 쓰면 데이터의 분포가 가우시안 분포이면 MSE를 사용하고 베르누이 분포면 cross-entropy를 사용한다.
진짜 마지막) what is cross entropy
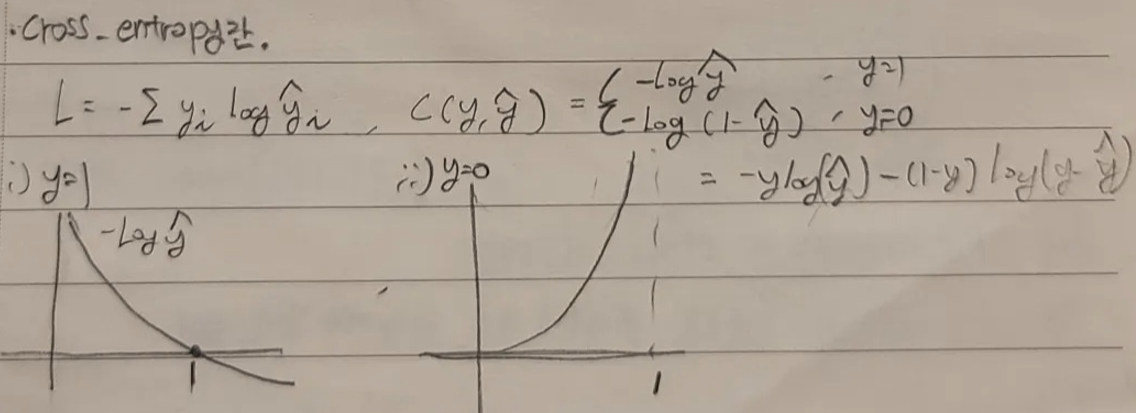
https://www.youtube.com/watch?v=34R_5FumoGw
딥러닝 모델 성늘 고도화 방법론들에 대해서 알아보자.
Drop Out
학습에 사용할 Node 중 랜덤으로 노이즈를 주어 학습이 진행되지 않게 한다. 학습이 완료시면 여러 모델을 앙상블시킨 것과 비슷한 효과가 나온다. 학습 때 뉴런을 무작위로 삭제하는 행위가 마치 매번 다른 모델을 학습시키는 것과 유사하기 때문이다.
구현

정규화
1) eature scalling
: 값의 범위를 맞추는 작업이다. 보통 [0,1] 사이로 맞춘다.
2) Batch Normalization
-motive) Vanishing Gradient Problem을 해결하기 위함. Vanishing Gradient Problem 이란 다음과 같다. 역전파 과정을 보면 미분을 하는 과정이 있다. activaton_function으로 sigmoid 함수를 사용할 경우 x값이 양 끝으로 갈수록 미분 값은 0에 수렴한다. 미분 값이 작아지면 파라미터 업데이트 정도가 낮아진다. 따라서 layer수가 많은 경우 뒤로 갈수록 업데이트가 급속도로 느려지는 문제를 말한다.
-functioning) 우선 batch 단위로 들어온 랜덤한 데이터들의 평균과 분산을 구한다. 각 데이터 마다 평균을 빼고 분산으로 나누면 전체 데이터들은 평균이 0이고 분산이 1인 분포를 따르게 된다. 이 분포를 x_i라고 하면 batch_normalization의 결과는
a*x_i + b가 된다. 이떄 a,b는 하이퍼 파라미터로 업데이트의 대상이다.
- meaning) 평균이 0이고 분산이 1인 분포로 만들어주는 작업은 랜덤한 데이터들을 모아서 중간 지점(x=0)에 뿌려주는 것을 의미한다. 이를 통해 미분 값이 0과 유사해지는 경우를 방지할 수 있다. 다만 무조건 0에만 뿌려주면 actvation_function을 사용하는 의미가 없어진다. linear한 상황이 되기 떄문이다. 그렇기에 h_parms를 부여해서 우선 0근처로 뿌려주되 이후 적당히 loss를 줄여주는 방향으로 분포를 이동시키는 작업을 수행한다.
-test dataset의 경우) test를 하는 경우에는 평균 값과 분산 값은 batch들의 평균들의 평균, 분산들의 평균을 사용한다.
-postion) 활성화 함수에 넣어주기 전에 적용한다.
-구현
class BatchNormalization:
def __init__(self, gamma, beta, momentum=0.9, running_mean = None, running_var = None) -> None:
self.gamma = gamma
self.beta = beta
self.momentum = momentum
#입력 데이터의 형태를 저장하기 위한 변수
self.input_shape = None
#테스트 상황에 사용할 평균과 분산
self.running_mean = running_mean
self.running_var = running_var
#역전파 과정에서 사용할 변수들
self.batch_size = None
self.xc = None
self.std = None
self.dgamma = None
self.dbeta = None일단 배치 정규화 예시에서 사용한 a,b가 gamma와 beta를 의미한다. momentum은 모든 데이터의 전반적인 평균, 분산을 구할 때 사용되는 값이다. input_shape는 입력 데이터의 형태를 저장하는데 반환할 때 원본 형태로 reshape 해주기 위해 사용된다.
running_mean/var가 되게 재밌는 변수들인데 테스트 상황에서는 보통 입력 데이터가 1개이다. 이 경우 mean/var를 구할 수 없기에 훈련 기간동안 running_mean/var을 업데이트하고 테스트 상황에 사용한다.
def forward(self,x,train_flag = True):
# 4D 텐서의 경우
if x.dim == 4:
N, C, H, W = x.shape
x = x.reshape(N,-1)
if self.running_mean is None:
N, D = x.shape
self.running_mean = np.zeros(D)
self.running_var = np.zeros(D)
if train_flag:
mu = x.mean(axis=0)
xc = x - mu
var = np.mean(xc**2, axis=0)
std = np.sqrt(var + 10e-7)
xn = xc / std
#중간 값을 저장
self.batch_size = x.shape[0]
self.xc = xc
self.xn = xn
self.std = std
self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu
self.running_var = self.momentum * self.running_var + (1-self.momentum) * var
else:
xc = x - self.running_mean
xn = xc / ((np.sqrt(self.running_var + 10e-7)))
output = self.gamma * xn + self.beta
return output.reshape(*self.input_shape)순전파의 코드이다. 설명했던 대로 평균을 구해서 데이터에서 빼주고 분산(std)를 구해서 나눠 xn을 만든다. running_mean/var이 어떠한 방식으로 업데이트 되는지를 유의깊게 보자.
advantage)
배치 정규화를 사용하면 GVP이 해결이 된다. 이전에는 layer 위치에 따라서 업데이트 되는 정도가 lr가 크면 컸어서 lr를 작게 설정해주어야 했는데 이제 배치 정규화를 사용하면 그런 문제가 해결되기에 맘놓고 lr를 크게 잡아도 된다.
3) 레이어 정규화
: Serial 데이터의 경우 batch 단위로 끊어주면 의미를 잃는 경우가 생김. ex) 문장
-> batch 단위가 아닌 Layer 별로 끊어주자
-> 대부분의 경우: 배치 정규화 / Serial 데이터 : 레이어 정규화 / 이미지 변환 : 인스턴스 정규화 / 나머지 : 그룹 정규화
가중치 초기화
아무렇게나 하이퍼 파라미터들을 초기화하면 아무 값이나 나온다...어떻게하면 효과적으로 가중치를 초기화 할 수 있을까.
-> 역사적인 내용은 생략
1) Xavier 초기화 <- 표준편차가 1/ np.sqrt(n)인 정규 분포로 초기화. 이렇게하면 적당히 넓게 고루 분포된 값을 초기 가중치 값들로 사용할 수 있다.
2) He 초기화 <- Xavier 방식이 다 좋은데 특정 활성화 함수들의 경우 미분값이 음수일 때 0이여서 layer가 깊어질수록 기울기 소실이 발생할 수 있다는 단점이 있다.이러한 단점을 해소하기 위해 가중치의 분포를 더 넓게(np.sqrt(2/n))한 정규 분포로 초기화하는 방식이 He 초기화이다.
cf) He(허)라고 읽는 사람들이 많더라고요 ㅋㅋ
-구현
class Net:
def __init__(self):
"""생략"""
def __init_weight(self, weight_init_std):
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1,all_size_list+1):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu','he'):
scale = np.sqrt( 2.0 / all_size_list[idx -1])
elif str(weight_init_std).lower() in ('sigmoid','xavier'):
scale = np.sqrt( 1.0 / all_size_list[idx -1])
#h_parms 초기화
self.params[f'W{idx}'] = scale * np.random.randn(all_size_list[idx-1],all_size_list[idx])
self.params[f'b{idx}'] = np.zeros(all_size_list[idx])
conclusion) 보통 a_funciont으로 sigmoid를 쓰면 Xavier 초기화를 하고 LeLU를 쓰면 He 초기화를 한다고 함.
가중치 감쇠
가능하다면 동일한 Loss라는 가정 하에 가중치가 낮은게 더 좋다는 직관을 기반으로 탄생한 기법.
Loss <- Loss + ratio_value * sigma(W^2)
학습 조기 종료
Training Loss가 감소함에도 너무 과하면 overfiiting이 일어나는데 이를 valudation Loss가 증가함을 근거로 알아차릴 수 있다. overfitting이 일어나면 조기 종료를 수행하도록 설정 가능하다.
마치며
인공뉴런의 개념을 이해하고 각 부분들의 작동 방식 등등을 알아보는 시간을 가져보았다.
